Consider the Finite Automaton below.




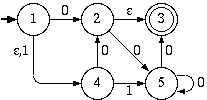
a.  Construct the smallest Deterministic Finite Automaton which accepts the same language.  Don't forget to include a dead state if there is nowhere to go in the non-deterministic machine from some state on some symbol. 


b.  Draw a regular expression that represents the language accepted by your machine.


c.  Write down a Regular (Linear) Grammar that generates it.

You must prove that your choice is correct. If regular, exhibit a machine, expression, or grammar;  if not regular, use the pumping lemma, and/or closure arguments.
 

1. The set of strings that have an even number of double zeros in them. (Note that three zeros in a row count as 2 double zeros).
2. The set of strings over the alphabet {0} of the form 0ⁿ where n is not a prime.
3. The set of all strings of the form xwx^R where x and w are non-empty strings over the alphabet {0,1}, and the big R over the x means the reverse of x.
4. The set of all strings over the alphabet {0} whose length is n! for some n > 0.
5. The set of all binary strings that read backwards the same as forwards (palindromes).
6. {www | w is a binary string}
7. {0^m1ⁿ | m is not equal to n}
8. {0^m1ⁿ0^m | m,n >= 0}
9. {0ⁱ1^j0^k | i,j,k >= 0,if i=1 then j=k}

Recall that a decision algorithm is an algorithm that returns a yes or no answer.   Give decision algorithms to determine if a Regular set


1. Has at least one string w that has 111 as a substring.
2. Is co-finite. (a set is co-finite if and only if its complement is finite).
3. Contains all strings of the form 0*1*

Recall that a right-linear grammar is one where every production is either in the from A->aB or A ->b, where a and b are terminal symbols. and A and B are non-terminal symbols. Every regular set can be generated by a right-linear grammar and every right-linear grammar generates a regular set.  Thus, a right-linear grammar is equivalent to a finite state machine, and we call a right-linear grammar regular..

a.  Write down a right-linear grammar to generate the set of strings that are evenly divisible by 5 when interpreted as a binary string.

b.  A left-linear grammar is a context-free grammar where each production must be either in the form A->Ba, or A->b, where a and b are terminal symbols and A and B are non-terminals.  Left-linear grammars are also equivalent to finite state machines. Explain how to convert a given finite state machine, to an equivalent left-linear grammar. You may use an example to illustrate.

Hint:  Let L be the language generated by some right-linear grammar G.  Reversing the right sides of each production in G creates a left linear grammar that generates the reverse of L.

1. Prove that every language of the form 0^mx+b, where m and b are non-negative integer constants and x ranges from 0 to infinite, is regular.
2. Describe a regular set over the alphabet {0} that is NOT of the form from part (a).
3. Extra Credit: Characterize all regular sets over the alphabet {0}, and prove your answer. That is, prove that every regular set over the alphabet {0} is of some particular form.

 Write a program to implement Hopcroft's FSM minimization algorithm that runs in O(n log n) time, in contrast to the O(n²) algorithm we described in class, known as Moore's algorithm.  Here is a nice place to look at some examples.