SchecterAdvancedMath

Trying to predict behavior is a basic goal of science. For example, when you throw a ball into the air at a certain speed, physicists can give you an equation that will predict exactly where the ball will be after a certain number of seconds.

Go do it! In particular, you can test a simple version of this equation yourself. Go to a high place with a stopwatch and look down to make sure there are no people below. Drop a small object like a rock or a penny (something that is not too effected by the wind), and simultaneously start the stopwatch. After t seconds the object will have dropped 16t² feet. Now of course the accuracy of this measurement depends on how carefully you read and press the stopwatch, and wind will interfere with a perfect calculation. Nevertheless, it is pretty cool that you can measure heights by a stopwatch! Let's say you are at the Grand Canyon, and your brother says - "Man I bet that drops off over 1000 feet!" You can check it by dropping a stone (make sure you are not over another trail - or your experiment will turn into a lesson on massive head injuries if the stonehits another hiker), and timing how many second it takes to hear it land. If it takes 5 seconds, that means the stone fell 16 x 5 x 5 = 400 feet. How long would it have to take to make the 1000 drop your brother envisioned? You would have to ask when is 16t² = 1000? The answer is when t equals the square root of 1000/16. This equals about 7.9 seconds. The predicting equation is called a quadratic equation and mankind has known all about solving quadratic equations since the Babylonians (1800 B.C.E. - the time of Avraham Avinu).

Physics is a great science because it is broadly able to predict many different phenomenon very accurately. Other areas of science have a harder time deriving precise equations. Some predictions are simply too hard to do perfectly and then we do the next best thing - find an equation that predicts pretty closely. The simplest kind of equation is a linear equation, and very often linear equations are used to approximately predict complex behavior.

The scientist takes his/her data and tries to reverse-engineer a linear equation from the data. You learned last lesson how to do this when you have two points of data. For example: let's say you are measuring the growth of a plant and on day 2 it is 4 inches high, and on day 5 it is 12 inches high. To get a linear function for this data, recall that we first calculate the slope. The slope is how much the plant grows divided by how much time has passed. In this case, the slope is 8/3. Then we set up an equation that looks like this: Height = (8/3) x Days. This means that every time we add a day, the plant will grow 8/3 inches, so that after 3 days it will have grown 8 imches. Now the plant may not be growing at a steady rate in which case our predcition of 8/3 inches per day will be off but it is a reasonable simple approximation. But we are not quite done yet, because when we put in 2 for Days, we get (8/3) x 2 = 16/3, and remember that the plant is actually 4 inches high not 16/3 inches. This discrepancy can be fixed by simply subtracting 4/3 inch. Hence our final equation would be:
Height = (8/3) x Days - 4/3.
Try it now for 5 just to check that we did not make any mistakes. We should get 12 inches, and indeed (8/3) x 5 - 4/3 = 12, which checks out correctly.

I believe that understanding exactly why things work in math is crucial. Sure you can get by pretty far by just imitating and memorizing methods, but you will never be able to apply the material to any new idea, and you will forever be the student whose abilities in math are restricted to imitating examples of things they have already seen. That kind of math is for computers and clever horses - not for humans. Don't be the kind of student who says or thinks "I never saw this before so I cannot do it". Instead, think "How does what I know and understand help me attack this new problem".

Now if you think this is hard up till now, I must remind you that up until now, the ideas and reasons about why and how everything works for linear functions, is within the grasp of any middle school student. If you still don't get it yet, then it is just a matter of practice, study, guidance, and time. Never give up. Never be satisfied with merely memorizing or imitating.

With that said however, we are about to enter a world that I am warning you in advance you will not be able to understand why everything works. You will still be able to understand how it works and actually use, appreciate and do the appropriate calculations, but the reasons why these methods are simply beyond the middle school world. I do not like to teach math this way - but in this case the practical use of the method you will learn, outweighs the pedagogical disadvantage of not being able to understand why it works.

So, go on to this next section forewarned that sometimes the complete picture in math will be over your head, and the best you can hope for is a mechanical approach. One day in 5-10 years when you are in college, you can come back and have a careful look at a field called linear algebra where you can study the concept of least squares solution to a set of normal equations.

Let's say that instead of two data points, we have 4 data points, but that no three points all lie on a straight line. In this case, we could take any pair of points (there are six different pairs - recall how to count choosing 2 from 4), and for each pair we would get a different linear equation. Each equation works for only two points and is off for the rest. For example, consider the points: (2, 4), (5, 12), (3, 4), and (1, 3), where the first number of each pair is the number of days elapsed and the second number is the height of the plant in inches. The equation Height = (8/3) x Days - 4/3 that works for (2, 4) and (5, 12) will not work for (1, 3) or (3, 4). Try it and see. When Days equals 1, we get (8/3) x 1 - 4/3 = 4/3 and that is not 3! When Days equals 3, we get (8/3) x 3 - 4/3 = 20/3, and that is not 4!

There is no single linear equation that will fit all the points, as surely as there is no straight line that runs through them all. If this is true, then what linear equation should we use? Here are some choices:
Pick any two points (6 possibilities) and use the equation that fits those two points exactly.
Find an equation that fits none of the points but somehow minimizes the cumulative error.

The best way to appreciate these possiblities is to look at a picture. The four points are drawn below. The line between (2, 4) and (5, 12) is shown, as well as another line that straddles all the points but hits none of them, and a red line that hits one point closely and misses the rest. Which one do you think is a better fit of the 4 points?

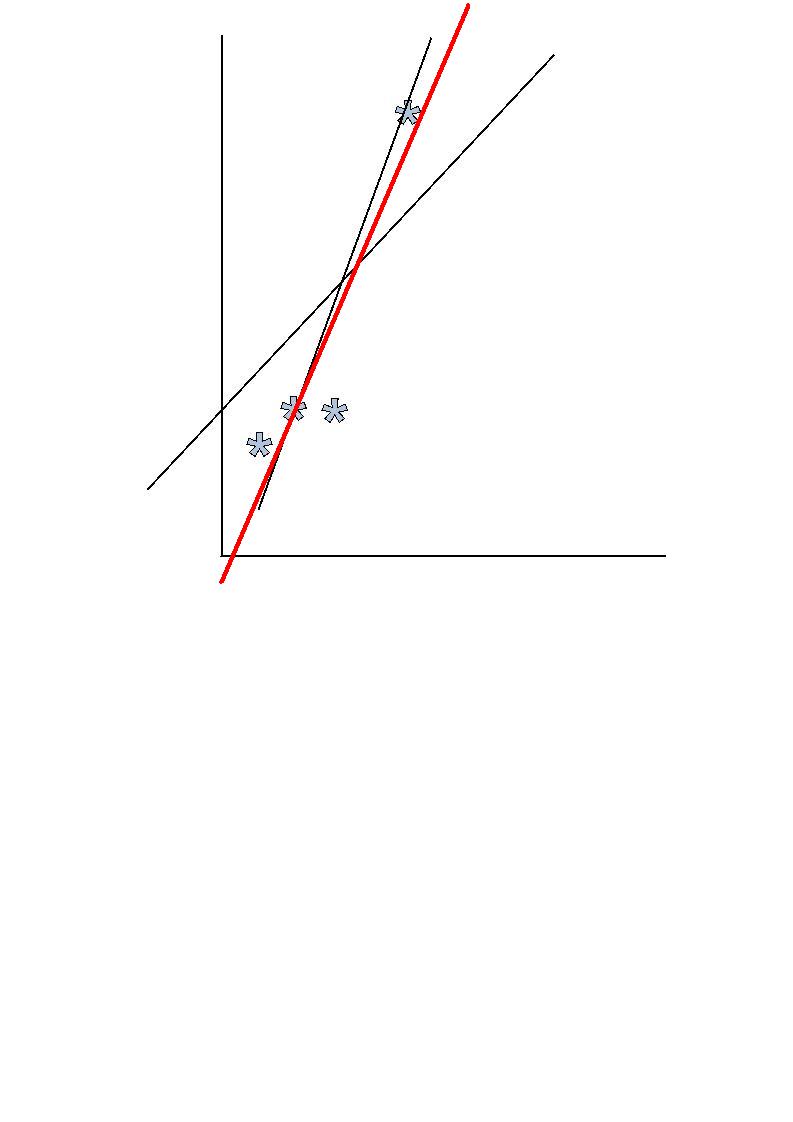
It is hard to decide what a better fit really means, so mathematicians came up with a definition that intuitively defines a line to be the best fit if it minimizes the sum of the squares of the distances to the data points. There are other defintions, one that uses the sum of the distances to the points, and one that uses the sum of the vertical distances to the points, but they are not the standard ones. Look here to explore the differences between these three definitions and to play with some examples yourself. You should look here for a simpler and friendlier exploring tool, and click on the gizmo for "Lines of Best Fit Using Least Squares".

The rest of this review is to show how to mechanically find the equation of the line that minimizes the sum of the squares of the distances, or the least squares solution. This is the black-box part of this review, which means that you will see how to do it, but the inner workings and the reasons why it works will remain for now a mystery.

Let's learn by an example in steps.

Let the four points be: (2, 4), (5, 12), (3, 4), and (1, 3).

Step 1:

From these points, construct two equations: 4x + 11y = 23 and 11x + 39y = 83. The 4 is because there are 4 points. The 11 is the sum of the first coordinates of the points. The 23 is the sum of the second coordinates of the points. The 39 is the sum of the squares of the first coordinates of the points, that is: 2x2 + 5x5 + 3x3 + 1x1. The 83 is the sum of the products of the coordinates of the points, that is: 2x4 + 5x12 + 3x4 + 1x3. I told you it would not make sense! But make sure you could still do it for any other set of points. Try it for (0, 1), (2, 7), (4, 9), (5, 10), (8, 20).

Step 2:

Find the point (x, y) that satisfies both equations. There are many ways to do this, and you may already have your favorite. The simplest way is to solve for x in terms of y in one equation, and then substitute the expression into the other expression. This effectively turns two equations and two unknowns into one equation and one unknown. In our example, the first equation gives x = (23-11y)/4. Substituting this into the second equation 11x + 39y = 83, gives 11 ((23-11y)/4) + 39y = 83. Simplifying gives (35/4) y = 79/4, and solving for y gives y = 79/35. You can go back to either equation to find that x = -16/35. Doublecheck this calculation by making sure that the values x = -16/35 and y = 79/35 satisfy both equations 4x + 11y = 23 and 11x + 39y = 83.

Step 3:

Draw the line Height = (79/35) Days - 16/35. This line is the best fit of the original points using the least squares method. It is shown in red above in the previous diagram.